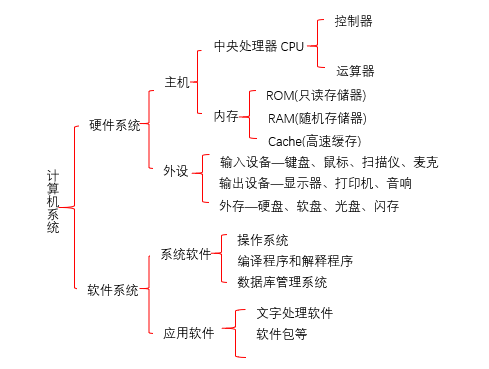
NOIP2012年普及组初赛题目及答案分析
一、单项选择题(共20题,每题1.5分,共计30分;每题且仅有一个正确选项)
1.计算机如果缺少(A ),将无法正常启动。
A.内存 B.鼠标 C. U盘 D. 摄像头
【分析】电脑缺少内存将无法启动,开机会黑屏。
2.( B)是一种先进先出的线性表。
A.栈 B.队列 C.哈希表(散列表) D.二叉树
【分析】
线性结构一般是一一对应,可以参考一次函数,非线性结构一般不是一次函数,参考二次函数。
A选项栈是一种先进后出的结构,
C选项哈希表也称为散列表(Hash 是根据关键码值(Key value)而直接进行访问的数据结构。
D选项二叉树是非线性结构
3.目前计算机芯片(集成电路)制造的主要原料是(A ),它是一种可以在沙子中提炼出的物质。
A.硅 B.铜 C.锗 D.铝
【分析】制作芯片的主要原料是硅(Si),沙子的主要成份(SiO2)
4.十六进制数9A在( B )进制下是232。
A.四 B.八 C.十 D.十二
【分析】
先把十六进制9A转换成十进制结果是89
A选项 转换成四进制是2122
B选项 转换成八进制232
C选项 转换成十进制是89
D选项转换成是十二进制10a
5.( C )不属于操作系统。
A.Windows B.DOS C.Photoshop D.NOI Linux
【分析】
A.是操作系统
B. DOS是磁盘操作系统(Disk Operating System),是早期个人电话上的一类操作系统。现在Windows还有它的影子。
C. Photoshop 是我们常说的PS软件,是照片处理软件。
D. NOI Linux 是基于linux的一个简单改版。
6.如果一棵二叉树的中序遍历是BAC,那么它的先序遍历不可能是( C )。
A.ABC B.CBA C.ACB D.BAC
【分析】中序遍历的规则是“左根右”,一棵二叉树可以没有左子树可以没有右子树,但是不能没有根结点。
当B作为根结点时,AC是右子树,先序遍历是BAC,D对。
当A作为根结点时,B是左子树,C是右子树,先序遍历是ABC,A对。
当C作为根结点是,BA是左子树,先序遍历是CBA ,B对。
7. 目前个人电脑的( B )市场占有率最靠前的厂商包括Intel、AMD等公司。
A.显示器 B.CPU C.内存 D.鼠标
【分析】Intel、AMD是生产CPU的厂商,目前常见的品牌型号有酷睿和锐龙。
8. 使用冒泡排序对序列进行升序排列,每执行一次交换操作系统将会减少1个逆序对,因此序列 5,4,3,2,1需要执行( C )次操作,才能完成冒泡排序。
A.0 B.5 C.10 D.15
【分析】首先明确一个问题,两个数比较大小,比较一次即可比较出来。
然后冒泡排序的主要代码如下:
for(int i=0 ; i<n-1; i==)
for(int j=0; j<n-1-i; j++)
主要思想是每次循环总是比较出一个最大值或者最小值,那么第一次比较4次即可,后面每比较一次就少一次,所以是4+3+2+1=10次
9. 1946年诞生于美国宾夕法尼亚大学的ENIAC属于( A )计算机。
A.电子管 B.晶体管 C.集成电路 D.超大规模集成电路
【分析】A、B、C、D分别代表计算机的四个时代,ENIAC是电子管时代。
10. 无论是TCP/IP模型还是OSI模型,都可以视为网络的分层模型,每个网络协议都会被归入某一层中。如果用现实生活中的例子来比喻这些“层”,以下最恰当的是( A)。
A. 中国公司的经理与波兰公司的经理交互商业文件

B. 军队发布命令

 C. 国际会议中,每个人都与他国地位对等的人直接进行会谈
C. 国际会议中,每个人都与他国地位对等的人直接进行会谈

D. 体育比赛中,每一级比赛的优胜者晋级上一级比赛

【分析】OSI模型和TCP/IP模型可以参考下面的模型,实际上,应用层和表示层等层之间会进行上下的数据交换,数据封装过程会有应用层到物理层,数据解封过程会有物理层到应用层。所以层和层上下之间也会存在箭头。

11.矢量图(Vector Image)图形文件所占的贮存空间比较小,并且无论如何放大、缩小或旋转等都不会失真,是因为它(B )。
A.记录了大量像素块的色彩值来表示图像
B.用点、直线或者多边形等基于数学方程的几何图元来表示图像
C.每个像素点的颜色信息均用矢量表示
D.把文件保存在互联网,采用在线浏览的方式查看图像
【分析】所谓矢量图,就是使用直线和曲线来描述的图形,构成这些图形的元素是一些点、线、矩形、多边形、圆和弧线等,它们都是通过数学公式计算获得的,具有编辑后不失真的特点。
矢量图的优点:
1.文件小,图像中保存的是线条和图块的信息,所以矢量图形文件与分辨率和图像大小无关,只与图像的复杂程度有关,图像文件所占的存储空间较小。
2.图像可以无限级缩放,对图形进行缩放,旋转或变形操作时,图形不会产生锯齿效果。
3.可采取高分辨率印刷,矢量图形文件可以在任何输出设备打印机上以打印或印刷的最高分辨率进行打印输出。
4.最大的缺点是难以表现色彩层次丰富的逼真图像效果。
5.矢量图与位图的效果是天壤之别,矢量图无限放大不模糊,大部分位图都是由矢量导出来的,也可以说矢量图就是位图的源码,源码是可以编辑的。
12. 如果一个栈初始时为空,且当前栈中的元素从栈顶到栈底依次为a,b,c,另有元素d已经出栈,则可能的入栈顺序是( D )。
A.a, d, c, b B.b, a, c, d C.a, c, b, d D.d, a, b, c
【分析】栈的特点是先进后出,栈顶到栈底分别是a,b,c。所以出栈顺序一定是a,b,c所有选项中只有D是符合a,b,c顺序的。
13.( B )是主要用于显示网页服务器或者文件系统的HTML文件的内容,并让用户与这些文件交互的一种软件。
A.资源管理器 B.浏览器 C.电子邮件 D.编译器
【分析】
A. 资源管理器是浏览电脑上的资源用的,文档视频照片等。
B.浏览器是用于浏览网页的工具。
C.电子邮件是网上收发邮件用的 。
D.编译器主要是用来编写和编译代码的。
14.( C )是目前互联网上常用的E-mail服务协议。
A.HTTP B.FTP C.POP3 D.Telnet
【分析】
A.选项是超文本传输协议
B. FTP是文件传输协议
C. POP3是E-mail协议
D. Telnet 是远程登录协议
15.( C )就是把一个复杂的问题分成两个或更多的相同类似的子问题,再把子问题分解成更小的子问题……直到最后的子问题可以简单地直接求解。而原问题的解就是子问题解的并。
A.动态规划 B.贪心 C.分治 D.搜索
【分析】
A选项动态规划是从全局考虑最终得出一个最优解,B选项贪心法,是从局部开始考虑出一个解,只是局部最优解,不一定是全局最优解。
C 选项分治的思想是把问题分而治之,把大化小。搜索算法就跟走迷宫一样,遇到路口就标记,直到找到出路。
16.地址总线的位数决定了CPU可直接寻址的内存空间大小,例如地址总线为16位,其最大的可寻址空间为64KB。如果地址总线是32位,则理论上最大可寻址的内存空间为( D )。
A.128KB B.1MB C.1GB D.4GB
【分析】计算规则 ,因为是1024,要计算32次方=* * * ,30次方是1GB,32次方是4GB
17.蓝牙和Wi-Fi都是( C )设备。
A.无线广域网 B.无线城域网 C.无线局域网 D.无线路由器
【分析】
都属于无限局域网
18. 在程序运行过程中,如果递归调用的层数过多,会因为( A )引发错误。
A.系统分配的栈空间溢出 B.系统分配的堆空间溢出
C.系统分配的队列空间溢出 D.系统分配的链表空间溢出
【分析】递归是调用栈,递归层数过多会引起栈空间溢出。
19. 原字符串中任意一段连续的字符所组成的新字符串称为子串。则字符“AAABBBCCC”共有( C )个不同的非空子串。
A.3 B.12 C.36 D.45
【分析】字串公式 最后一个加1表示加了空字串,去掉后是45,但是,观察原字符串可以发现 第一个A和第二个A还有第三个A是同一个字符串,说明这45个中肯定有重复的。A,B,C各重复两个,45-6=39。前三个A中,第一个和第二个A组成的AA,还有第二个和第三个组成的AA重复,同理BB和CC也重复一个,所以39-3=36个。
20. 仿生学的问世开辟了独特的科学技术发展道路。人们研究生物体的结构、功能和工作原理,并将这些原理移植于新兴的工程技术中。以下关于仿生学的叙述,错误的是( B )
A.由研究蝙蝠,发明雷达 B.由研究蜘蛛网,发明因特网
C.由研究海豚,发明声纳 D.由研究电鱼,发明伏特电池
【分析】ACD都是仿生学的具体应用,只有B没有仿生学的依据。
二、问题求解(共2题,每题5分,共计10分)
1. 如果平面上任取n个整点(横纵坐标都是整数),其中一定存在两个点,它们连线的中点也是整点,那么n至少是______5____。
【分析】需要从坐标角度考虑,平面上的点可以分成x坐标和y坐标,点1(x1,y1),点2(x2,y2), 点3(x3,y3)……这些x和y全部按照题目描述的都是整数,那么平面上所有的点坐标情况可以有以下几种
(奇数,奇数)
(偶数,偶数)
(奇数,偶数)
(偶数,奇数)
现在要求连线的中点也是偶数,也就是上面描述的情况,也就是需要任意点连线的中点也是偶数,就是是偶数,也是偶数。那么运气最好的时候,可以选两个同种类型的点(上面其中任何一种),如果运气不好的情况下, 那么上面这四种都选了,这个时候还没有出现重复的类型,这个时候任意给一个点,一定会跟上面的四种情况之一有重复,从而符合题目要求,所以至少是5点。
2. 在NOI期间,主办单位为了欢迎来自各国的选手,举行了盛大的晚宴。在第十八桌,有5名大陆选手和5名港澳选手共同进膳。为了增进交流,他们决定相隔就坐,即每个大陆选手左右旁都是港澳选手,每个港澳选手左右旁都是大陆选手。那么,这一桌一共有___2880____种不同的就坐方案。
注:如果在两个方案中,每个选手左右相邻的选手相同,则视为同一种方案。
【分析】考察圆桌排列,题目要求港澳台选手旁是大陆选手,可以先让大陆选手或者港澳台选手左下,这个时候是圆桌排列,公式。 然后坐好后剩余5个空,让大陆选手或者港澳台选手插空即可。A(5,5)。所以是 *A(5,5)
三、阅读程序写结果。(共4题,每题8分,共计32分)
1 2 3 4 5 6 7 8 9 10 11 | #include <iostream>using namespace std;int a,b,c,d,e,ans;int main() { cin>>a>>b>>c; d=a+b; e=b+c; ans=d+e; cout<<ans<<endl; return 0;} |
输入:1 2 5
输出:___10____
【分析】
题目本身不难,简单模拟即可,a=1,b=2,c=5。d=a+b=3, e=b+c =7, ans= d+e =10
2.
1 2 3 4 5 6 7 8 9 10 11 12 | #include <iostream>using namespace std;int n,i,ans;int main(){ cin>>n; ans=0; for(i=1;i<=n;i++) if(n%i==0) ans++; cout<<ans<<endl; return 0; } |
输入:18
输出:___6___
【分析】比较简单,可以简单模拟出来,输入是18,当i=1,2,3,6,9 ,18 一共6个数,实际上是求输入n后,把n约数的个数输出。
3.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | #include <iostream>using namespace std;int n,i,j,a[100][100];int solve(int x,int y){ int u,v; if(x==n) return a[x][y]; u=solve(x+1,y); v=solve(x+1,y+1); if(u>v) return a[x][y]+u; else return a[x][y]+v; }int main(){ cin>>n; for(i=1;i<=n;i++) for(j=1;j<=i;j++) cin>>a[i][j]; cout<<solve(1,1)<<endl; return 0; } |
5
2
-1 4
2 -1 -2
-1 6 4 0
3 2 -1 5 8
输出:______________
【分析】做题当中常遇到的递归调用。按照以下的流程图考虑。

| y=1 | y=2 | y=3 | y=4 | y=5 | |
| x=1 | 14 | 12 | 8 | 8 | 8 |
| x=2 | 9 | 12 | 8 | 8 | 8 |
| x=3 | 10 | 8 | 7 | 8 | 8 |
| x=4 | 2 | 8 | 9 | 8 | 8 |
| x=5 | 3 | 2 | -1 | 5 | 8 |
这个题目要求solve(1,1)。但是题目中x的值为5的时候有返回值。
solve(5,5)=a[5][5]=8, solve(5,4)=a[5][4]=5,
依次类推可以填写完上面的表格。但是注意一点,计算solve(4,5) 的时候,由于没有直接的返回值,需要计算u和v。u=solve(5,5) ,v=solve(5,6) 。
这个时候因为a[5][6]没有直接赋值,而a数组是全局变量,没有赋值默认为0。实际上,有很多数字都是没有用的,上面标红的数据没有实际作用,可以不用求解。
4.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | #include <iostream>#include <string>using namespace std;int n,i,j,ans;string s;char get(int i) { if(i<n) return s[i]; else return s[i-n];}int main() { cin>>s; n=s.size(); ans=0; for(i=1; i<=n-1; i++) { for(j=0; j<=n-1; j++) if(get(i+j)<get(ans+j)) { ans=i; break; } else if(get(i+j)>get(ans+j)) break; } for(j=0; j<=n-1; j++) cout<<get(ans+j); cout<<endl; return 0;} |
输入:CBBADADA
输出:____________
【分析】
为了便于求解先把get函数求出来,
get(0)=C, get(1)=B, get(2)=B, get(3)=A, get(4)=D, get(5)=D, get(6)=D, get(7)=A,
get(8)=C, get(9)=B, get(10)=B……
| i | i<=n-1 | j | j<=n-1 | if(get(i+j)<get(ans+j)) | ans | else if(get(i+j)> get(ans+j)) |
| 1 | 1<=7 | 0 | 0<=7 | get(1)<get(0),成立 | 1 | |
| 2 | 2<=7 | 0 | 0<=7 | get(2)<get(1),不成立 | get(2)>get(1),不成立 | |
| 1 | 1<=7 | get(3)<get(2),成立 | 2 | |||
| 3 | 3<=7 | 0 | 0<=7 | get(3)<get(2),成立 | 3 | |
| 4 | 4<=7 | 0 | 0<=7 | get(4)<get(3),不成立 | get(4)>get(3),成立 | |
| 5 | 5<=7 | 0 | 0<=7 | get(5)<get(3),成立 | 5 | |
| 6 | 6<=7 | 0 | 0<=7 | get(6)<get(5),不成立 | get(6)>get(5),成立 | |
| 7 | 7<=7 | 0 | 0<=7 | get(7)<get(5),不成立 | get(7)>get(5),不成立 | |
| 1 | 1<=7 | get(8)<get(6),成立 | 7 |
知道了ans,就可以输出 (ans+j)
四、完善程序(前2空每空2分,后8空每空3分,共计28分)
1.(坐标统计)输入n个整点在平面上的坐标。对于每个点,可以控制所有位于它左下方的点(即x、y坐标都比它小),它可以控制的点的数目称为“战斗力”。依次输出每个点的战斗力,最后输出战斗力最高的点的编号(如果若干个点的战斗力并列最高,输出其中最大的编号)。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | #include <iostream>using namespace std;const int SIZE =100;int x[SIZE],y[SIZE],f[SIZE];int n,i,j,max_f,ans;int main() { cin>>n; for(i=1; i<=n; i++) cin>>x[i]>>y[i]; max_f=0; for(i=1; i<=n; i++) { f[i]= ① ; for(j=1; j<=n; j++) { if(x[j]<x[i] && ② ) ③ ; } if( ④ ) { max_f=f[i]; ⑤ ; } } for(i=1; i<=n; i++) cout<<f[i]<<endl; cout<<ans<<endl; return 0;} |
【分析】
f数组是战斗力,题目要求输出每个点的战斗力,
①【 0 】 每次循环之前战斗力数组要重置为0。
②【 y[j]< y[i] 】 因为要统计左下角的点,也就是说x2和y2都要小于x1和y1,点1才能拥有点2的战斗力。
③ 【 f[i]++ 】 战斗力增加
④ 【 f[i] >= max_f】 当前要比较出最大战斗力和坐标值
⑤【 ans= i】 把当前的位置编号赋值给ans注意:此题经过查询网络上流程的版本,第四个空和第五个空有的答案有如下版本
④【 (i>1)&& (f[i]>f[i-1])】
⑤ ans=max_f
2.(排列数)输入两个正整数n,m(1<n<20,1<m<n),在1~n中任取m个数,按字典序从小到大输出所有这样的排列。例如:
输入:3 2
输出:1 2
1 3
2 1
2 3
3 1
3 2
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 | #include <iostream>#include <cstring>using namespace std;const int SIZE =25;bool used[SIZE];int data[SIZE];int n,m,i,j,k;bool flag;int main() { cin>>n>>m; memset(used,false,sizeof(used)); for(i=1; i<=m; i++) { data[i]=i; used[i]=true; } flag=true; while(flag) { for(i=1; i<=m-1; i++) cout<<data[i]<<" "; cout<<data[m]<<endl; flag= ① ; for(i=m; i>=1; i--) { ② ; for(j=data[i]+1; j<=n; j++) if(!used[j]) { used[j]=true; data[i]= ③ ; flag=true; break; } if(flag) { for(k=i+1; k<=m; k++) for(j=1; j<= ④ ; j++) if(!used[j]) { data[k]=j; used[j]=true; break; } ⑤ ; } } } return 0;} |
【分析】
① 【 false 】下面有将flag赋值为 true的过程,所以这个空应该初始化为false。
② 【 used[data[i]]=flase 】 used表示使用过的数据,这个地方data[i] 没有使用过,所以设置为false。
③ 【 j 】 如果j没有使用过,那么就把它放到data里。
④【 n】 这个地方是在枚举操作,枚举n个数。
⑤【 break 】 完成了任务直接退出即可。
扫描二维码推送至手机访问。
版权声明:本文由青少年编程知识记录发布,如需转载请注明出处。