【题目描述】

一群孩子做游戏，现在请你根据游戏得分来发糖果，要求如下：

1. 每个孩子不管得分多少，起码分到一个糖果。

2. 任意两个相邻的孩子之间，得分较多的孩子必须拿多一些糖果。(若相同则无此限制)

给定一个数组 arrarr 代表得分数组，请返回最少需要多少糖果。

【输入描述】

一行，包含n个数

【输出描述】

一行一个数，表示最少需要多少糖果

【样例输入1】

1 1 2

【样例输出1】

4

【样例1解释】

最优分配方案为1 1 2

【样例2输入】

1 1 1

【样例2输出】

3

【样例2解释】

最优分配方案是1,1,1

【思路】

要想分出最少的糖果，利用贪心思想，肯定是相邻位置没有增加的情况下，大家都分到1，相邻位置有增加的情况下，分到糖果数加1就好。什么情况下会增加糖果，相邻位置有得分差异，可能是递增可能是递减，如果是递增的话，糖果依次加1，如果是递减糖果依次减1？这不符合最小，因为减到最后一个递减的位置可能不是1，必须从1开始加才是最小，那我们可以从最后一个递减的位置往前反向加1.

【做法】

• step 1：使用一个辅助数组记录每个位置的孩子分到的糖果，全部初始化为1.

• step 2：从左到右遍历数组，如果右边元素比相邻左边元素大，意味着在递增，糖果数就是前一个加1，否则保持1不变。

• step 3：从右到左遍历数组，如果左边元素比相邻右边元素大， 意味着在原数组中是递减部分，如果左边在上一轮中分到的糖果数更小，则更新为右边的糖果数+1，否则保持不变。

• step 4：将辅助数组中的元素累加求和。

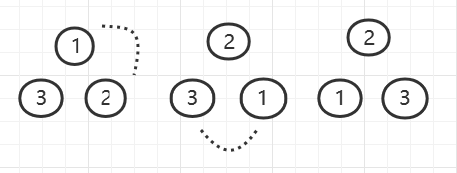
【图示】

【参考答案】

#include <iostream>
using namespace std;

const int MAX_SIZE = 1000; // 假设数组长度不超过1000

int candy(int arr[], int n) {
    if (n <= 1)
        return n;

    int nums[MAX_SIZE];
    // 初始化
    for (int i = 0; i < n; i++)
        nums[i] = 1;

    // 从左到右遍历
    for (int i = 1; i < n; i++) {
        // 如果右边在递增，每次增加一个
        if (arr[i] > arr[i - 1])
            nums[i] = nums[i - 1] + 1;
    }

    // 记录总糖果数
    int res = nums[n - 1];

    // 从右到左遍历
    for (int i = n - 2; i >= 0; i--) {
        // 如果左边更大但是糖果数更小
        if (arr[i] > arr[i + 1] && nums[i] <= nums[i + 1])
            nums[i] = nums[i + 1] + 1;

        // 累加和
        res += nums[i];
    }

    return res;
}

int main() {
    int arr[] = {1, 2, 2}; // 示例输入
    int n = sizeof(arr) / sizeof(arr[0]);
    cout << candy(arr, n) << endl; // 输出结果
    return 0;
}