【题目描述】

小X的老师很喜欢围棋。众所周知，围棋的棋盘有19行19列，共有361个交叉点。为方便起见，我们把这些行列按顺序编号为1～19，并用(x, y)表示第x列第y行的位置。例如下图中，A用(16,4)表示，B用(14, 3)表示。
小X在做一个机器人的项目，他正思考这样一个问题：如果一个小机器人从(x1, y1)这个位置出发，沿直线移动到(x2, y2)这个位置，它一共经过了多少个交叉点？
注意起点和终点也算作经过，因此至少经过了2个交叉点。

【输入描述】

输入数据仅有一行包含4个用空格隔开的正整数，分别表示x1, y1, x2, y2

【输出描述】

输出一行包含一个小于20的正整数，表示从(x1, y1)沿直线移动到(x2, y2)经过的交叉点的个数。

【样例输入】

4 4 4 16

【样例输出】

13

【提示】

样例输入
样例1:
4 4 4 16
样例2:
1 1 19 19
样例3:
1 1 7 5
样例输出
样例1:
13
样例2:
19
样例3:
3
样例解释3
经过了(1, 1), (4, 3), (7, 5)共3个交叉点，你在图上画条直线就能一目了然看出来。

【数据范围】

对于20%的数据，x1=x2
对于另外20%的数据，y1=y2
对于另外30%的数据，满足abs(x1-x2)=abs(y1-y2)，它们是某个正方形的两个对角顶点
对于100%的数据，1<=x1, y1, x2, y2<=19

【题目分析】

1. 题目出的不错，挖了一些坑，稍有难度。

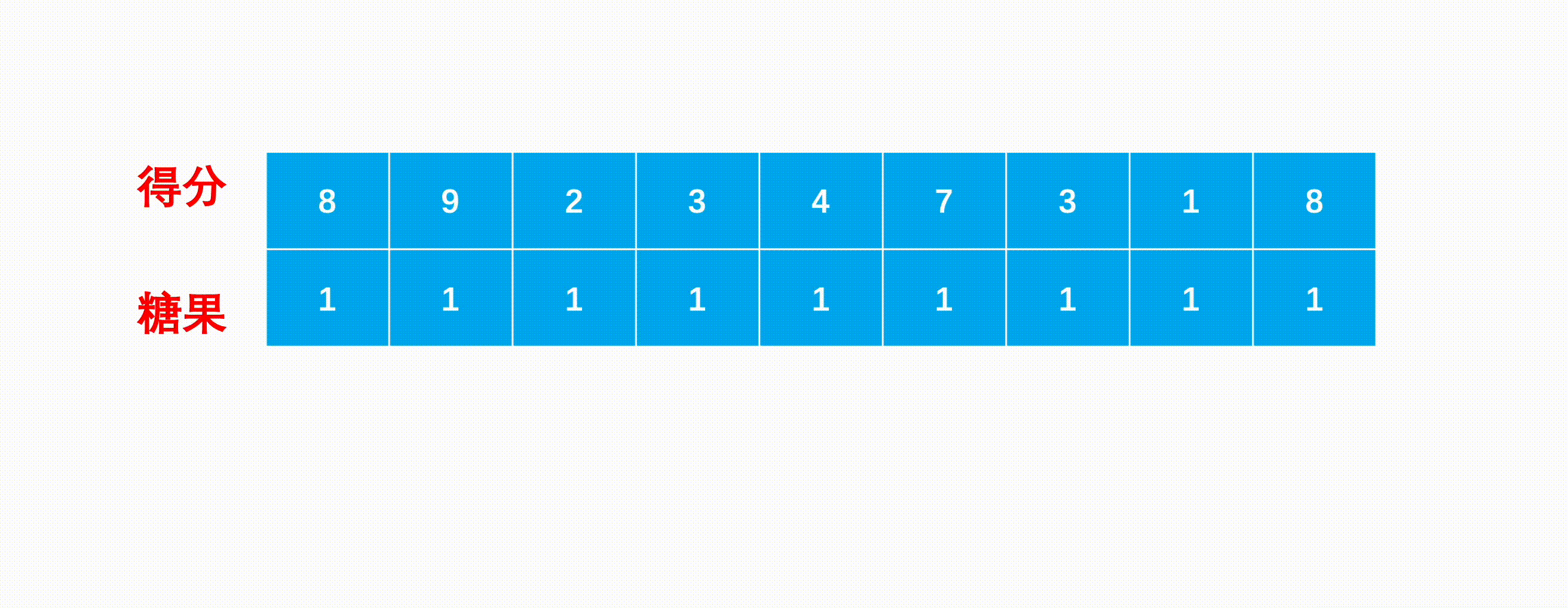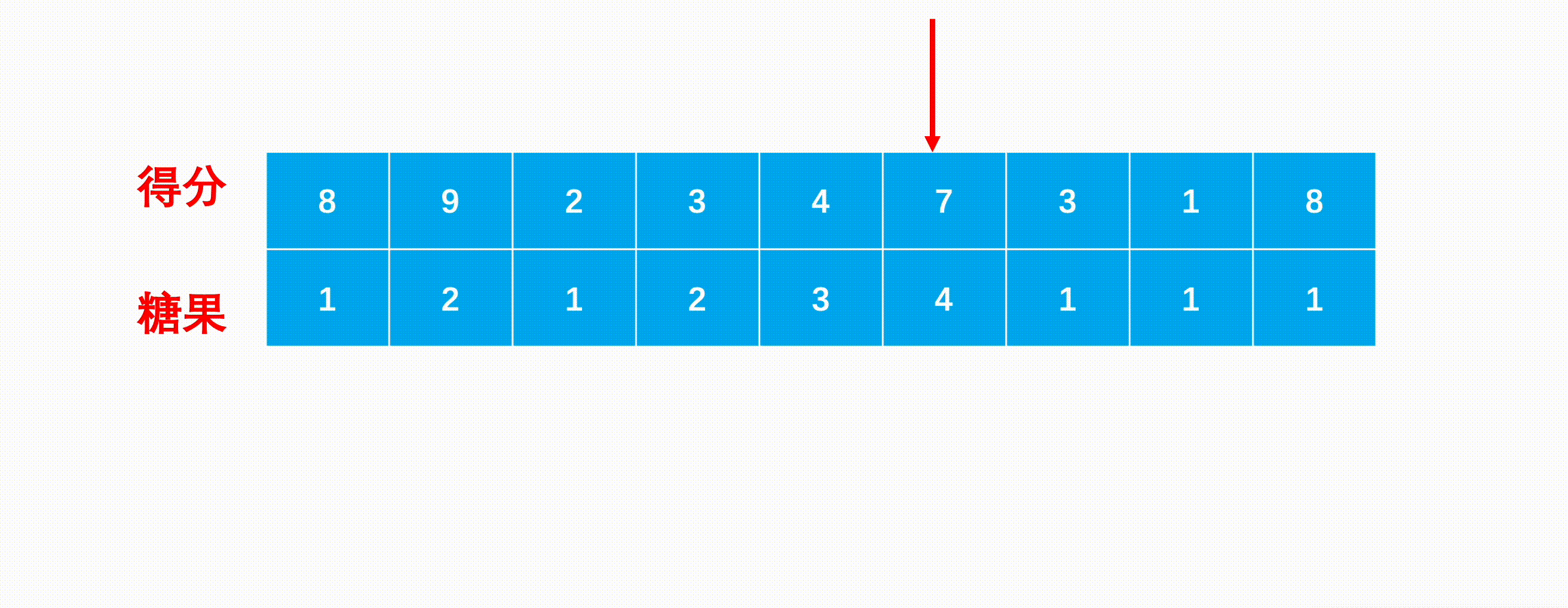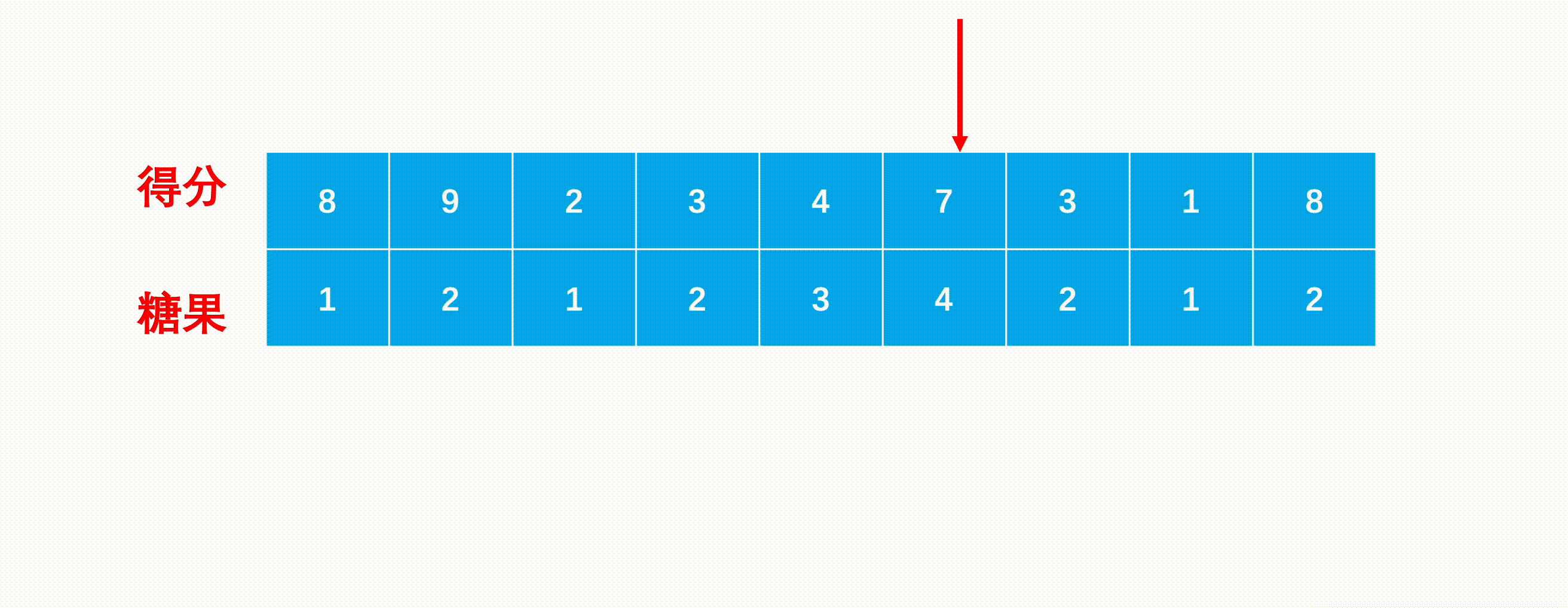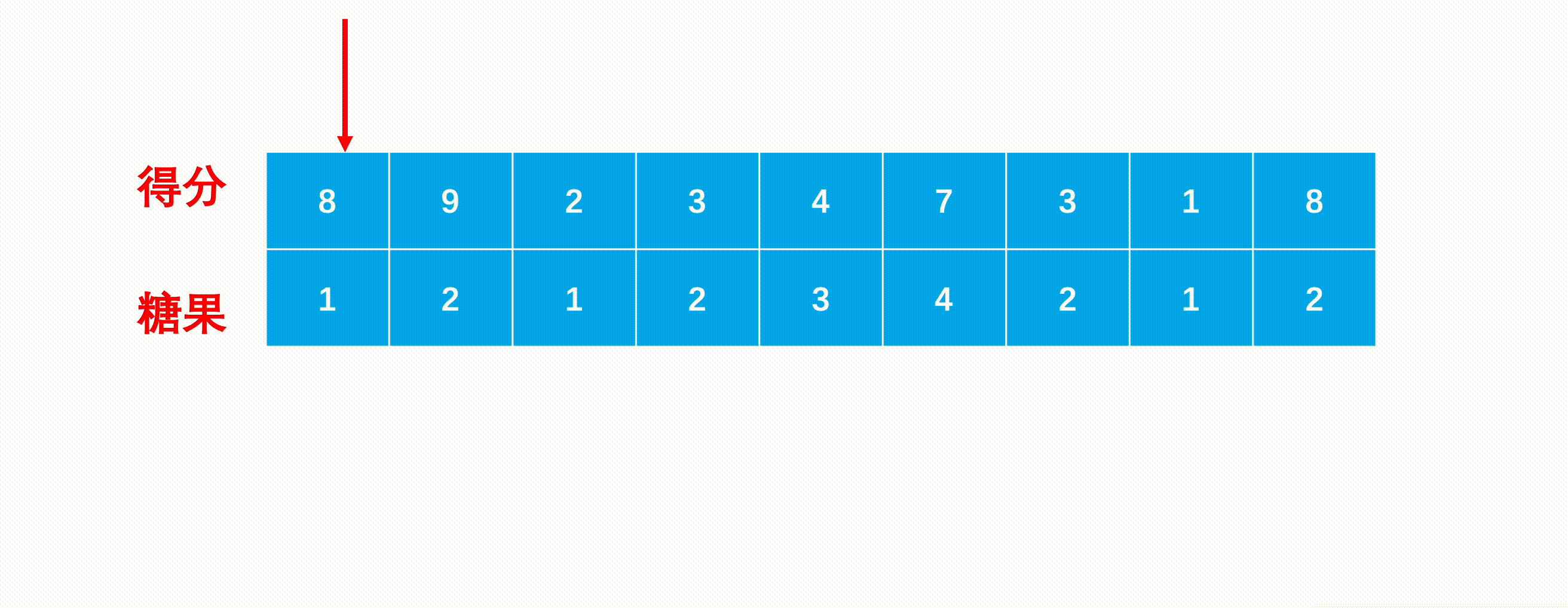
2. 分析样例 4 4  4 16 如下图：

一共经历13个点。

然后 1 1 7 5 这两个坐标

这是题目所解释的，带有开头和结尾的点，加上中间（4，3）这个点，正好落在“交叉”点上。所以答案一共3个点。

如何判断是否正好有坐标点在两个点给定的直线上?

题目中x轴的差是6，y轴的差是4。

【参考答案1】——网络答案

核心思路：枚举每一步向某个方向走一格后另一格的长度。怎么用整形判断点呢？没错，可以用分数表达。我们设i为走的格子数，a是两点间x轴距离，b是两点间y轴距离（绝对值），如果b*i%a==0成立（分数表达法）

#include<bits/stdc++.h>
using namespace std;
int main()
{
	int x1,y1,x2,y2;
	scanf("%d%d%d%d",&x1,&y1,&x2,&y2);
	int a,b,s=1;
	a=abs(x2-x1);//x轴差
	b=abs(y2-y1);//y轴差
	if(a<b)//我们选择大的枚举格子数
	{
		swap(a,b);
	}
	for(int i=1;i<=a;i++)//开始枚举
	{
		if(b*i%a==0)//判断分数形式的数值是否为整数
		{
			s++;//累加答案
		}
	}
	printf("%d\n",s);
	return 0;
}

【参考答案2——点与直线的关系】

1. 由两个点可以构造直线公式，判断是否有符合条件的点在此直线上。

    确定两点，如何构造一条直线。

   假设点A(x1,y1)，点B(x2,y2)是平面直角坐标系上的两点，则这两点组成的直线方程是

        (y-y2)/(y1-y2) = (x-x2)/(x1-x2)

    假如用题目中的1 1 7 5 代入得：

  (y-1)/4 = (x-1)/6

化简得：y=(x+1)/3

判断 1 1  7 5  下方所有的点是否在此直线上即可。

使用双重for循环遍历最长的边组成的方形，内层循环套入此公式，只要得出的结论对外层循环取余为0就是符合题目要求的。